 算法笔记(2)
算法笔记(2)
# 5、链表
链表
https://www.yiibai.com/python/py_data_structure/python_linked_lists.html
https://codingdict.com/article/4838
2
3
# 5.1 节点
在有些情况下,存储数据的内存分配不能位于连续的内存块中。所以我们接受指针的帮助,其中数据和数据元素的下一个位置的地址也被存储。所以我们从当前数据元素的值中知道下一个数据元素的地址。通常这样的结构被称为指针。但在Python中,我们将它们称为节点。
节点是各种其他数据结构链接列表和发can可以在python中处理的基础。
每个节点包含两部分,数据域item和指向下一个节点的指针next
"""
在有些情况下,存储数据的内存分配不能位于连续的内存块中。所以我们接受指针的帮助,其
中数据和数据元素的下一个位置的地址也被存储。所以我们从当前数据元素的值中知道下一个数据元素的地址。
通常这样的结构被称为指针。但在Python中,我们将它们称为节点。
"""
class Node(object):
"""节点: 数据域、指针"""
def __init__(self, item):
self.item = item # 数据域
self.next = None # 下一个节点
# 1、创建节点
n1 = Node(1)
n2 = Node(2)
n3 = Node(3)
n4 = Node(4)
# 2、连接节点
n1.next = n2
n2.next = n3
n3.next = n4
# 3、遍历节点节点
traverse_node = n1
while traverse_node:
print(traverse_node.item)
traverse_node = traverse_node.next
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 5.2 单链表
# 5.2.1 链表的概念
链表是一种物理存储上非连续,数据元素的逻辑顺序通过链表中的指针链接次序,实现的一种线性存储结构。由一系列`节点`组成的元素集合。每个节点包含两部分,
链表是由一系列节点组成的元素集合。每个节点包含两部分,数据域item和指向下一个节点的指针next。通过节点之间的相互连接,最终串成一个链表。

# 5.2.2 创建链表
我们通过节点对象传递适当的值来指向下一个数据元素进行连接
"""
链表是由一系列节点组成的元素集合。每个节点包含两部分,数据域item和指向下一个节点的指针next。
通过节点之间的相互连接,最终串成一个链表。
创建一个Node对象并创建另一个类来使用这个Node对象
"""
class Node(object):
"""节点: 数据域、指针"""
def __init__(self, item):
self.item = item # 数据域
self.next = None # 下一个节点
class LinkedList(object):
"""一个链表是由一系列节点组成"""
def __init__(self):
self.linked_list = None
# 1、创建节点
n1 = Node(1)
n2 = Node(2)
n3 = Node(3)
n4 = Node(4)
# 2、连接节点(节点添加到链表中) n1 -> n2 -> n3 通过节点的互相连接形成一个链表
link = LinkedList()
link.linked_list = n1 # 链表添加n1节点(首节点)
link.linked_list.next = n2 # 给next添加n2节点
n2.next = n3 # n2节点next跟n3
n3.next = n4
# 3、获取节点(节点连接后就可以从n1获取到n3了,变的有关系了)
print(link.linked_list.item)
print(link.linked_list.next.item)
print(link.linked_list.next.next.item)
print(link.linked_list.next.next.next.item) # 没有节点时: AttributeError: 'NoneType' object has no attribute 'item'
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# 5.2.3 遍历链表
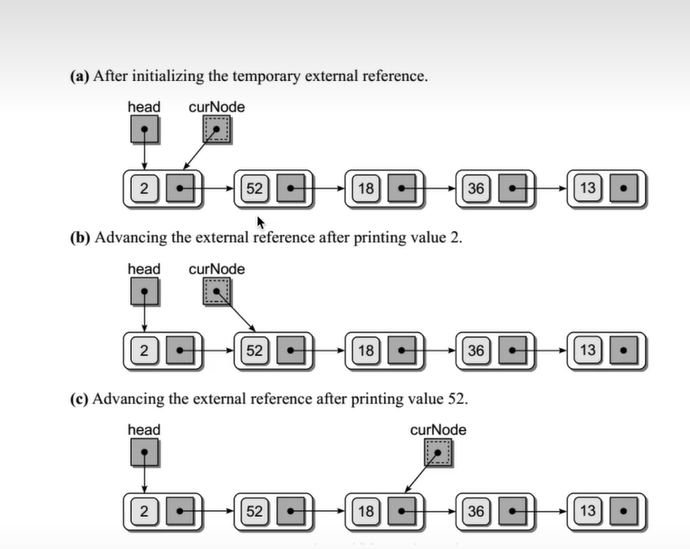
从第一个数据元素开始。我们只需通过将下一个节点的指针指向当前数据元素来打印下一个数据元素的值。
- item获取到值,next重新指向下一个节点
"""
从第一个数据元素开始。我们只需通过将下一个节点的指针指向当前数据元素来打印下一个数据元素的值。
"""
class Node(object):
"""节点: 数据域、指针"""
def __init__(self, item):
self.item = item # 数据域
self.next = None # 下一个节点
class LinkedList(object):
"""一个链表是由一系列节点组成"""
def __init__(self):
self.linked_list = None
def list_print(self):
"""遍历节点"""
print_val = self.linked_list
while print_val is not None:
print(print_val.item)
print_val = print_val.next
# 1、创建节点
n1, n2, n3, n4 = Node(1), Node(2), Node(3), Node(4)
# 2、连接节点 n1 -> n2 -> n3 -> n4
link = LinkedList()
link.linked_list = n1
link.linked_list.next = n2
n2.next = n3
n3.next = n4
# 3、遍历链表
link.list_print()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 5.2.4 插入链表
在链表中插入元素涉及将指针从现有节点重新分配给新插入的节点。取决于新数据元素是在链表的开始位置还是在中间位置或末尾插入
头插法
将新数据节点的下一个指针指向链表的当前头部。因此,链表的当前头成为第二个数据元素,新节点成为链表的头部。
需要知道插入节点的头head
def create_link_head(self, element):
"""头插入节点"""
current_node = Node(element) # 新节点
current_node.next = self.linked_list # 将新节点的下一个元素指到原链表前面
self.linked_list = current_node # 重新赋值链表
2
3
4
5
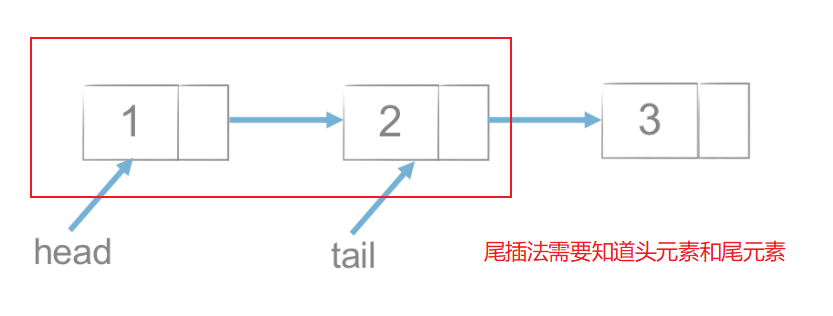
尾插法
将链表的当前最后一个节点的下一个指针指向新的数据节点。因此链表的当前最后一个节点成为倒数第二个数据节点,新节点成为链表的最后一个节点。
创建节点,如果当前链表为空则直接添加,否则循环链表直接最后一个节点在添加
def create_link_tail(self, element):
"""尾插入节点"""
current_node = Node(element) # 新节点
if self.linked_list is None: # 如果链表中没有节点则直接添加
self.linked_list = current_node
return
last_node = self.linked_list
while last_node.next: # 直接找到最后一个节点,然后在添加到链表中
last_node = last_node.next
last_node.next = current_node
2
3
4
5
6
7
8
9
10
11
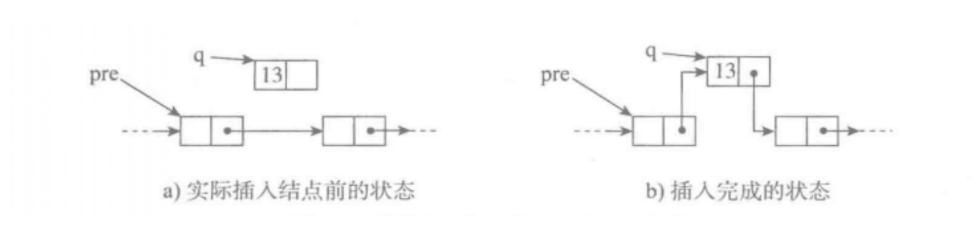
中间插入
将指定节点 pre 指针指向新节点 q 。将新节点 q 的下一个指针改变为指定节点 pre 的下一个指针。
一定注意需要先断开节点,在进行重新连接
def create_link_in_between(self, middle_node, element):
"""在指定位置插入节点"""
if middle_node is None:
print('指定节点不存在,找不到插入节点位置')
current_node = Node(element)
current_node.next = middle_node.next # 先断开节点,在连接(先连接就会出错,一定记住先断开)
middle_node.next = current_node # 在重新指向middle_node的节点
2
3
4
5
6
7
示例
"""
头插入
新数据节点的下一个指针指向链表的当前头部。因此,链表的当前头成为第二个数据元素,新节点成为链表的头部
尾插入
创建节点,如果当前链表为空则直接添加,否则循环链表直接最后一个节点在添加
中间插入
将指定节点 **pre** 指针指向新节点 **q** 。将新节点 **q** 的下一个指针改变为指定节点 **pre** 的下一个指针。
"""
class Node(object):
"""节点: 数据域、指针"""
def __init__(self, item):
self.item = item # 数据域
self.next = None # 下一个节点
class LinkedList(object):
"""一个链表是由一系列节点组成"""
def __init__(self):
self.linked_list = None
def list_print(self):
"""遍历节点"""
print_val = self.linked_list
while print_val is not None:
print(print_val.item, end=' ')
print_val = print_val.next
def create_link_head(self, element):
"""头插入节点"""
current_node = Node(element) # 新节点
current_node.next = self.linked_list # 将新节点的下一个元素指到原链表前面
self.linked_list = current_node # 重新赋值链表
def create_link_tail(self, element):
"""尾插入节点"""
current_node = Node(element) # 新节点
if self.linked_list is None: # 如果链表中没有节点则直接添加
self.linked_list = current_node
return
last_node = self.linked_list
while last_node.next: # 直接找到最后一个节点,然后在添加到链表中
last_node = last_node.next
last_node.next = current_node
def create_link_in_between(self, middle_node, element):
"""在指定位置插入节点"""
if middle_node is None:
print('指定节点不存在,找不到插入节点位置')
current_node = Node(element)
current_node.next = middle_node.next # 先断开节点,在连接(先连接就会出错,一定记住先断开)
middle_node.next = current_node # 在重新指向middle_node的节点
# 1、创建节点
n1, n2, n3, n4 = Node(1), Node(2), Node(3), Node(4)
# 2、连接节点 n1 -> n2 -> n3 -> n4
link = LinkedList()
link.linked_list = n1
link.linked_list.next = n2
n2.next = n3
n3.next = n4
# 3、头插入
link.create_link_head(5) # 5 1 2 3 4
# 4、尾插入
link.create_link_tail(6) # 5 1 2 3 4 6
# 5、指定节点插入
link.create_link_in_between(n3, 99) # 5 1 2 3 99 4 6
# 6、遍历链表
link.list_print()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
# 5.2.5 删除列表
找到要删除的节点的前一个节点。然后将该节点的下一个指针指向要删除的节点的下一个节点
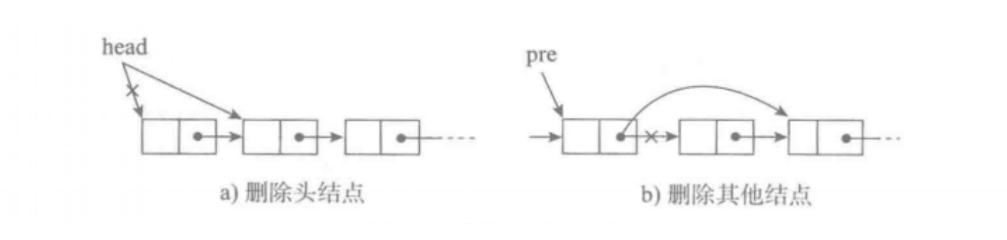
- 删除头节点 链表重新指向第二个元素 self.linked_list = head_node.next
- 删除尾节点 head_node=None
- 删除其他节点 删除节点的上一个节点直接重新指向删除节点的后一个节点previous_node.next = head_node.next
"""
找到要删除的节点的前一个节点。 然后将该节点的下一个指针指向要删除的节点的下一个节点。
删除的是头节点
删除的是尾节点
删除的是其他节点
"""
class Node(object):
"""节点: 数据域、指针"""
def __init__(self, item):
self.item = item # 数据域
self.next = None # 下一个节点
class LinkedList(object):
"""一个链表是由一系列节点组成"""
def __init__(self):
self.linked_list = None
def list_print(self):
"""遍历节点"""
print_val = self.linked_list
while print_val is not None:
print(print_val.item, end=' ')
print_val = print_val.next
def remove_node(self, element):
"""删除元素"""
head_node = self.linked_list # 得到链表
if head_node is not None: # 1、如果是删除的是链表的第一个节点,则直接链表指向下一个节点
if head_node.item == element:
self.linked_list = head_node.next
return
while head_node is not None:
if head_node.item == element: # 找到元素退出循环
break
previous_node = head_node # 记录上一个节点
head_node = head_node.next # 记录当前节点
if head_node is None: # 2、如果删除的是最后一个节点,head_node=None
return
# 3、删除的是其他节点,上一个节点越过删除节点重新连接到删除后面的节点
previous_node.next = head_node.next
n1, n2, n3, n4 = Node(1), Node(2), Node(3), Node(4)
# 2、连接节点 n1 -> n2 -> n3 -> n4
link = LinkedList()
link.linked_list = n1
link.linked_list.next = n2
n2.next = n3
n3.next = n4
# 3、删除节点
link.remove_node(4)
# 4、遍历链表
link.list_print()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
# 5.2.6 其他操作
https://jackkuo666.github.io/Data_Structure_with_Python_book/chapter3/section1.html
单链表的操作
- is_empty() 链表是否为空
- length() 链表长度
- travel() 遍历整个链表
- add(item) 链表头部添加元素
- append(item) 链表尾部添加元素
- insert(pos, item) 指定位置添加元素
- remove(item) 删除节点
- search(item) 查找节点是否存在
"""
- is_empty() 链表是否为空
- length() 链表长度
- travel() 遍历整个链表
- add(element) 链表头部添加元素
- append(element) 链表尾部添加元素
- insert(pos, element) 指定位置添加元素
- remove(element) 删除节点
- search(element) 查找节点是否存在
- update(modify_node,element) 修改指定节点
"""
class Node(object):
"""节点: 数据域、指针"""
def __init__(self, item):
self.item = item # 数据域
self.next = None # 下一个节点
class LinkedList(object):
"""一个链表是由一系列节点组成"""
def __init__(self):
self._linked_list = None
def is_empty(self):
"""判断链表是否为空"""
return self._linked_list is None
def length(self):
"""链表长度"""
length = 0
head_node = self._linked_list
while head_node is not None:
length = length + 1
head_node = head_node.next
return length
def travel(self):
"""遍历整个链表"""
head_node = self._linked_list
while head_node is not None:
print(head_node.item, end=' ')
head_node = head_node.next
def add(self, element):
"""从链表头部插入元素"""
current_node = Node(element)
current_node.next = self._linked_list
self._linked_list = current_node
def append(self, element):
"""从链表尾部插入元素"""
current_node = Node(element)
if self._linked_list is None:
self._linked_list = current_node
return
head_node = self._linked_list
while head_node.next:
head_node = head_node.next
head_node.next = current_node
def insert(self, pos, element):
"""指定位置插入元素,输入下标插入0开始"""
if pos <= 0: # 1、如果下标小于等于0则插入到链表最前面
self.add(element)
return
elif pos > self.length() - 1: # 2、插入的位置大于链表,则插入到队尾
self.append(element)
else: # 3、在链表中间插入元素
count = 0
head_node = self._linked_list
current_node = Node(element)
while count < pos - 1: # count大于插入位置 停止循环插入节点
count = count + 1
head_node = head_node.next
current_node.next = head_node.next # 先连接后面的节点,在连接前面节点
head_node.next = current_node
def remove(self, element):
"""删除指定节点"""
head_node = self._linked_list
if head_node is not None: # 如果删除的元素在头节点
if head_node.item == element:
self._linked_list = head_node.next
return
while head_node is not None: # 如果删除的节点在尾节点
if head_node.item == element:
break
previous_node = head_node # 记录上一个节点
head_node = head_node.next
if head_node is None:
return
previous_node.next = head_node.next # 删除的节点在中间,直接上一个节点重新指向删除的后一个节点
def search(self, element):
"""查找某个节点是否存在"""
if self._linked_list is None:
return False
head_node = self._linked_list
while head_node is not None:
if head_node.item == element:
return True
head_node = head_node.next
return False
def update(self, modify_node, element):
"""修改指定节点"""
if modify_node is None:
raise IndexError('节点不存在')
head_node = self._linked_list
while head_node is not None:
if head_node.item == modify_node.item:
head_node.item = element
break
head_node = head_node.next
n1, n2, n3, n4 = Node(1), Node(2), Node(3), Node(4)
link = LinkedList()
link._linked_list = n1
link.add(2)
link.add(3)
link.append(5)
link.insert(0, 8) # 在链表的第几个位置插入 0 链表开始节点插入
link.insert(90, 88) # 链表最后面插入
link.insert(1, 100) # 链表2下标后面插入元素
link.update(n1, 111)
print('查找某个节点是否存在: ', link.search(11))
print("链表是否为空(True: 空): ", link.is_empty())
print("链表长度: ", link.length())
link.travel() # 遍历链表
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
# 5.3 单项循环链表
https://jackkuo666.github.io/Data_Structure_with_Python_book/chapter3/section2.html
单链表的一个变形是单向循环链表,链表中最后一个节点的next域不再为None,而是指向链表的头节点。
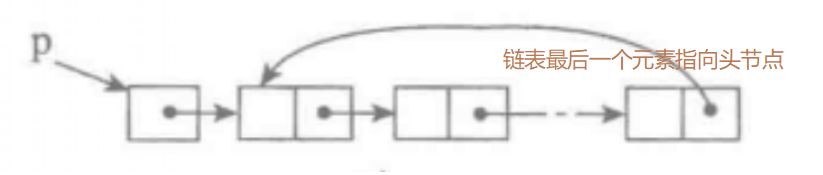
"""
- is_empty() 链表是否为空
- length() 链表长度
- travel() 遍历整个链表
- add(element) 链表头部添加元素
- append(element) 链表尾部添加元素
- insert(pos, element) 指定位置添加元素
- remove(element) 删除节点
- search(element) 查找节点是否存在
- update(modify_node,element) 修改指定节点
单链表的一个变形是单向循环链表,链表中最后一个节点的next域不再为None,而是指向链表的头节点
"""
class Node(object):
"""节点: 数据域、指针"""
def __init__(self, item):
self.item = item # 数据域
self.next = None # 下一个节点
class LinkedList(object):
"""一个链表是由一系列节点组成"""
def __init__(self):
self._linked_list = None
def is_empty(self):
"""判断链表是否为空"""
return self._linked_list is None
def length(self):
"""链表长度"""
if self.is_empty(): # 链表为空直接返回0
return 0
length = 1 # 初始值是1表示while循环的时候是比较当前的下一个节点
head_node = self._linked_list
# 重点就是换掉这个: 当最后一个节点的下一个节点不等于首节点则循环(单向循环链表就是首尾相连)
while head_node.next != self._linked_list:
length = length + 1
head_node = head_node.next
return length
def travel(self):
"""遍历整个链表"""
if self.is_empty():
return
head_node = self._linked_list
print(head_node.item, end=' ')
while head_node.next != self._linked_list:
print(head_node.next.item, end=' ')
head_node = head_node.next
def add(self, element):
"""从链表头部插入元素"""
current_node = Node(element)
if self.is_empty():
self._linked_list = current_node # 只有一个节点首位相连
current_node.next = self._linked_list
return
current_node.next = self._linked_list # 1、先将节点的下一个连接到链表
head_node = self._linked_list
while head_node.next != self._linked_list: # 跳出循环则表示到了最后一个节点
head_node = head_node.next
head_node.next = current_node # 2、在将最后一个节点连接到首节点,形成循环
self._linked_list = current_node
def append(self, element):
"""从链表尾部插入元素"""
current_node = Node(element)
if self.is_empty():
self._linked_list = current_node # 只有一个节点首位相连
current_node.next = self._linked_list
return
head_node = self._linked_list
while head_node.next != self._linked_list: # 跳出循环则表示到了最后一个节点
head_node = head_node.next
current_node.next = self._linked_list # 1、先将插入节点连接到首节点
head_node.next = current_node # 2、在将原来最后一个节点重新指向插入尾部的节点
def insert(self, pos, element):
"""指定位置插入元素,输入下标插入0开始"""
if pos <= 0: # 1、如果下标小于等于0则插入到链表最前面
self.add(element)
return
elif pos > self.length() - 1: # 2、插入的位置大于链表,则插入到队尾
self.append(element)
else: # 3、在链表中间插入元素
count = 0
head_node = self._linked_list
current_node = Node(element)
while count < pos - 1: # 跳出循环则找到需要插入的位置
count = count + 1
head_node = head_node.next
# 先断开在连接
# 先连接后面的节点(插入节点的下一个节点,连接到指定位置的下一个节点),在连接前面节点
current_node.next = head_node.next
head_node.next = current_node
def remove(self, element):
"""删除指定节点"""
if self.is_empty():
return
# 1、删除的节点是链表的首节点
head_node = self._linked_list
if head_node.item == element:
# 表示有多个节点
if head_node.next != self._linked_list:
while head_node.next != self._linked_list:
head_node = head_node.next # 跳出循环,到了尾节点
# 尾节点的下一个重新指向删除节点的后一个节点,并重新赋值self._linked_list = self._linked_list.next
head_node.next = self._linked_list.next
self._linked_list = self._linked_list.next
else:
# 表示只有一个节点
self._linked_list = None
else:
previous_node = None # 默认上一个节点
while head_node.next != self._linked_list:
if head_node.item == element:
previous_node.next = head_node.next # 找到则重新指向节点(跳过删除节点)
return
previous_node = head_node
head_node = head_node.next
# 当跳出循环: 删除的元素在最后一个
if head_node.item == element:
previous_node.next = self._linked_list
def search(self, element):
"""查找某个节点是否存在"""
if self.is_empty():
return False
head_node = self._linked_list
while head_node.next != self._linked_list:
if head_node.item == element:
return True
head_node = head_node.next
return False
def update(self, modify, element):
"""修改指定节点"""
modify_node = Node(modify)
if not self.search(modify):
raise IndexError('修改节点不在其链表中')
head_node = self._linked_list
while head_node.next != self._linked_list:
if head_node.item == modify_node.item:
head_node.item = element
break
head_node = head_node.next
n1, n2, n3, n4 = Node(1), Node(2), Node(3), Node(4)
link = LinkedList()
link.add(2)
link.add(1)
link.append(3)
link.append(5)
link.insert(1, 8)
link.update(1, 111)
print('查找某个节点是否存在: ', link.search(111))
print("链表是否为空(True: 空): ", link.is_empty())
print("链表长度: ", link.length())
link.travel() # 遍历链表
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
# 5.4 双链表
一种更复杂的链表是“双向链表”或“双面链表”。每个节点有两个链接:一个指向前一个节点,当此节点为第一个节点时,指向空值;而另一个指向下一个节点,当此节点为最后一个节点时,指向空值。
- 双链表的第一个节点的前一个节点prior为None
- 双链表的第最后一个节点的后一个节点next为None
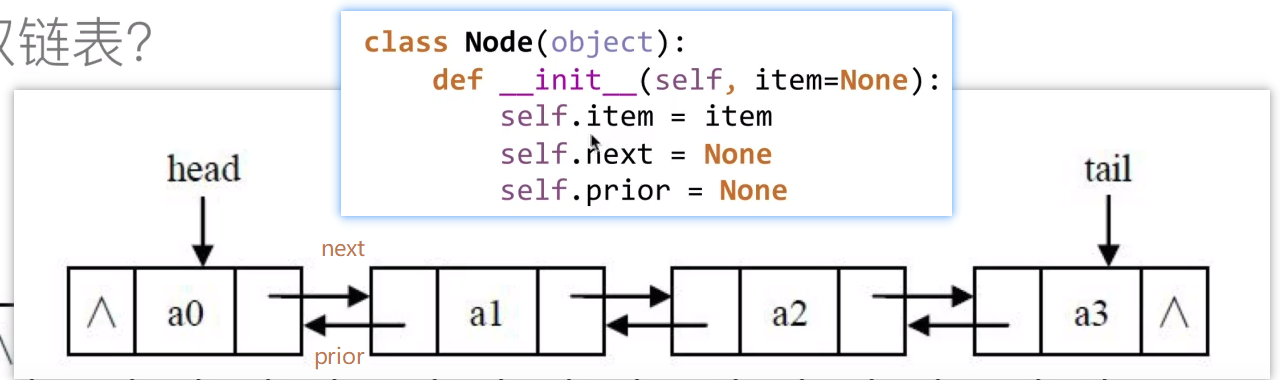
# 5.4.1 指定位置插入节点
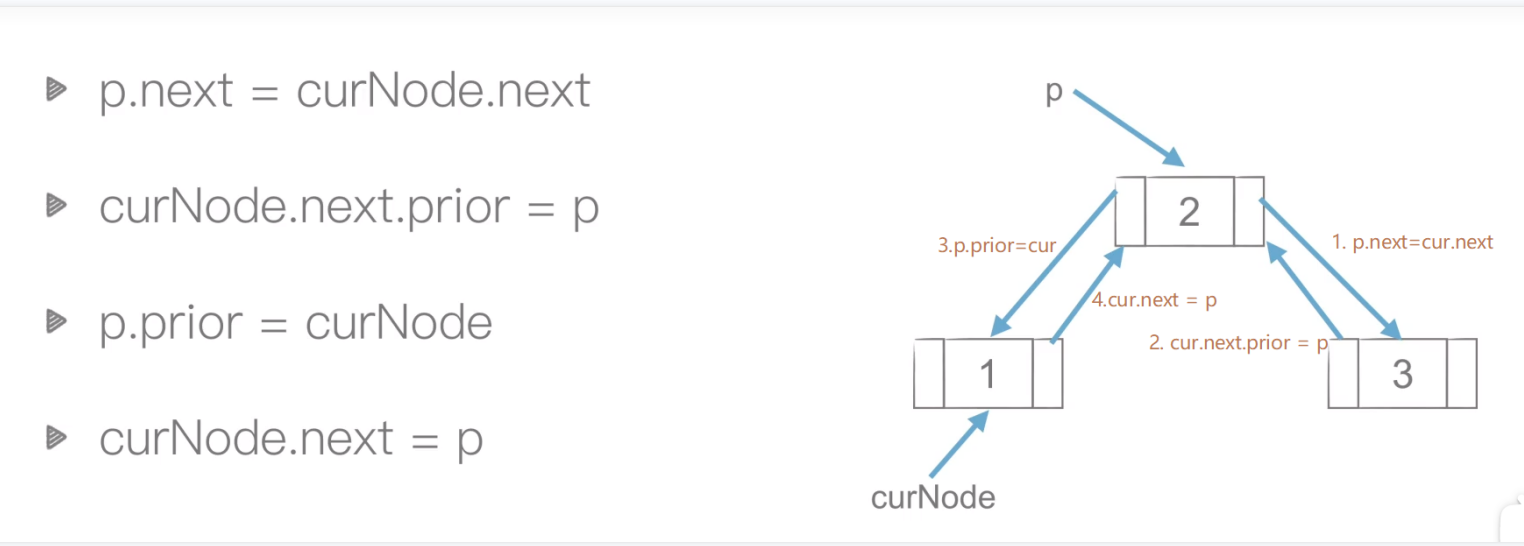
相应实现方法
"""
- is_empty() 链表是否为空
- length() 链表长度
- travel() 遍历整个链表
- add(element) 链表头部添加元素
- append(element) 链表尾部添加元素
- insert(pos, element) 指定位置添加元素
- remove(element) 删除节点
- search(element) 查找节点是否存在
- update(modify_node,element) 修改指定节点
每个节点有两个链接:
一个指向前一个节点,当此节点为第一个节点时,指向空值;
而另一个指向下一个节点,当此节点为最后一个节点时,指向空值
"""
class Node(object):
"""节点: 数据域、指针"""
def __init__(self, item):
self.item = item # 数据域
self.next = None # 下一个节点
self.prior = None # 上一个节点
class LinkedList(object):
"""一个链表是由一系列节点组成"""
def __init__(self):
self._linked_list = None
def is_empty(self):
"""判断链表是否为空"""
return self._linked_list is None
def length(self):
"""链表长度"""
if self.is_empty(): # 链表为空直接返回0
return 0
length = 0
head_node = self._linked_list
while head_node is not None: # head_node等于None表示最后一个节点
length = length + 1
head_node = head_node.next
return length
def travel(self):
"""遍历整个链表"""
if self.is_empty():
return
head_node = self._linked_list
while head_node is not None:
print(head_node.item, end=' ')
head_node = head_node.next
def add(self, element):
"""从链表头部插入元素
1、先将新节点的下一个(next)指向链表的头节点
2、原链表的头节点上一个(prior)指向到新节点
3、链表重新赋值指向新节点
"""
current_node = Node(element)
if self.is_empty():
self._linked_list = current_node
return
current_node.next = self._linked_list # 1、先将节点的下一个连接到链表
self._linked_list.prior = current_node # 2、原链表的头节点上一个(prior)指向到新节点
self._linked_list = current_node # 3、赋值
def append(self, element):
"""从链表尾部插入元素
1、原链表最后一个节点的下一个节点(next)指向新节点
2、新节点的上一个节点(prior)指向原链表的最后一个节点
"""
current_node = Node(element)
if self.is_empty():
self._linked_list = current_node
return
head_node = self._linked_list
while head_node.next is not None: # 跳出循环则表示到了最后一个节点
head_node = head_node.next
head_node.next = current_node # 1、最后一个节点的下一个节点(next)指向新节点
current_node.prior = head_node # 2、新节点的上一个节点(prior)指向原最后一个节点
def insert(self, pos, element):
"""指定位置插入元素,输入下标插入
1、如果下标小于等于0则插入到链表最前面
2、插入的位置大于链表,则插入到队尾
3、在链表中间插入元素
3.1 将新节点的next指向head_node的next
3.2 将head_node的next的prior指向新节点
3.3 将新节点的prior指向head_node
3.4 将head_node的下一个节点指向新节点
"""
if pos <= 0: # 1、如果下标小于等于0则插入到链表最前面
self.add(element)
return
elif pos > self.length() - 1: # 2、插入的位置大于链表,则插入到队尾
self.append(element)
else: # 3、在链表中间插入元素
count = 0
head_node = self._linked_list
while count < pos - 1: # 跳出循环则找到需要插入的位置
count = count + 1
head_node = head_node.next
current_node = Node(element) # 新插入节点
# 先断开在连接,先插入节点连接后面的节点,在连接前面节点
# 1、将新节点的next指向head_node的next
current_node.next = head_node.next
# 2、将head_node的next的prior指向新节点
head_node.next.prior = current_node
# 3、将新节点的prior指向head_node
current_node.prior = head_node
# 4、将head_node的下一个节点指向新节点
head_node.next = current_node
def remove(self, element):
"""删除指定节点
1、第一个就是删除的元素
如果只有一个节点
"""
if self.is_empty():
return
head_node = self._linked_list
# 1、第一个就是删除的元素
if head_node.item == element:
if head_node.next is None: # 如果只有一个节点
self._linked_list = None
return
else:
head_node.next.prior = None # 当前节点的下一个节点的prior为None
self._linked_list = head_node.next
return
while head_node is not None: # 如果删除的节点不是首节点
if head_node.item == element:
# 2、链表中中间的节点
if head_node.next is not None:
# 将cur的前一个节点的next指向cur的后一个节点
head_node.prior.next = head_node.next
# 将cur的后一个节点的prev指向cur的前一个节点
head_node.next.prior = head_node.prior
break
else:
# 3、删除链表中最后一个节点
head_node.prior.next = None
head_node.prior = None
head_node = head_node.next
# if head_node is None:
# return
def search(self, element):
"""查找某个节点是否存在"""
if self.is_empty():
return False
head_node = self._linked_list
while head_node is not None:
if head_node.item == element:
return True
head_node = head_node.next
return False
def update(self, modify, element):
"""修改指定节点"""
modify_node = Node(modify)
if not self.search(modify):
raise IndexError('修改节点不在其链表中')
head_node = self._linked_list
while head_node is not None:
if head_node.item == modify_node.item:
head_node.item = element
break
head_node = head_node.next
link = LinkedList()
link.add(2)
link.add(1)
link.append(3)
link.append(5)
link.insert(2, 8)
link.update(1, 111)
link.remove(2)
print('查找某个节点是否存在: ', link.search(111))
print("链表是否为空(True: 空): ", link.is_empty())
print("链表长度: ", link.length())
link.travel() # 遍历链表
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
# 5.5 链表与顺序表(python的列表)的对比
链表失去了顺序表随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大,但对存储空间的使用要相对灵活。
链表与顺序表的各种操作复杂度如下所示:
| 操作 | 链表 | 顺序表 |
|---|---|---|
| 访问元素 | O(n) | O(1) |
| 在头部插入/删除 | O(1) | O(n) |
| 在尾部插入/删除 | O(n) | O(1) |
| 在中间插入/删除 | O(n) | O(n) |
注意虽然表面看起来复杂度都是 O(n),但是链表和顺序表在插入和删除时进行的是完全不同的操作。链表的主要耗时操作是遍历查找,删除和插入操作本身的复杂度是O(1)。顺序表查找很快,主要耗时的操作是拷贝覆盖。因为除了目标元素在尾部的特殊情况,顺序表进行插入和删除时需要对操作点之后的所有元素进行前后移位操作,只能通过拷贝和覆盖的方法进行。
# 5、算法进阶
# 5.1 贪心算法
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出当前看来是最好的选择。也就是说,不从整体最优上加以考虑,它所做出的是某种意义上的局部最优解**。
贪心算法并不保证会得到最优解,但是在某些问题上贪心算法的解就是最优解。要会判断一个问题能否用贪心算法来计算。
# 1. 贪心算法基础示例-找零问题
假设商店老板需要找零n元钱,钱币的面额有:100、50、20、5、1,如何找零使得所需钱币的数量最少?
贪心结论:从最大的面额开始找
"""
假设商店老板需要找零n元钱,钱币的面额有:100、50、20、5、1,如何找零使得所需钱币的数量最少?
思路:
从最大的开始找,从最大的取余
生成一个列表t,和money列表想对应,【1,0,0,0,0,0】 表示有一个一百的面额
遍历列表,对后面的数取余
"""
money = [100, 50, 20, 10, 5, 1] # 面额
def give_change(m):
"""
找零
:param m: 找零总数
:return: 钱币数量
"""
t = [0 for _ in range(len(money))] # 生成一个列表t,和money列表想对应,【1,0,0,0,0,0】 表示有一个一百的面额
for idx, val in enumerate(money):
t[idx] = m // val
m = m % val
print('面额', t)
return sum(t)
print('面额总数', give_change(269))
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 2. 贪心算法基础示例-背包问题
一个小偷在某个商店有n个商品,第i个商品价值vi元,重wi千克。他希望拿走的价值尽量高,但他的背包最多只能容纳W千克的东西。他应该拿走那些商品?
- 0-1背包:对于一个商品,小偷要么把它完整拿走,要么留下。不能只拿走一部分,或把一个商品拿走多次。(商品为金条)
- 分数背包:对于一个商品,小偷可以拿走其中任意一部分。(商品为金砂)
- 贪心结论:得到商品每千克的单价,通过单价进行排序,如果背包剩余部分小于商品的重量,则可以拿走其一部分

# a. 0-1背包
# b. 分数背包
"""
一个小偷在某个商店有n个商品,第i个商品价值vi元,重wi千克。他希望拿走的价值尽量高,但他的背包最多只能容纳W千克的东西。他应该拿走那些商品?
- **分数背包**:对于一个商品,小偷可以拿走其中任意一部分。(商品为金砂)
商品 单价 重量/千克
A 60 10
B 100 20
C 120 30
思路:
1、解决这个问题主要是,需要计算出商品每千克最划算的商品,所有先计算出商品每千克的单价
2、背包重量大于最优商品重量,则全部拿走
3、背包重量小于最优商品重量,则拿走背包剩余容量的商品
"""
goods = [(60, 10), (100, 20), (120, 30)] # 商品
goods.sort(key=lambda x: x[0] / x[1], reverse=True) # 计算商品每千克的单价
def fractional_backpack(goods, w):
"""
分数背包
:param goods: 排序好的商品
:param w: 小偷背包重量
:return: 最优装了多少前
"""
total_value = 0 # 小偷拿走的总价值
m = [0 for _ in range(len(goods))]
for idx, (price, weight) in enumerate(goods):
# 1、背包重量大于最优商品重量,则全部拿走
if w >= weight:
m[idx] = 1 # 全部拿走这个商品
total_value = total_value + price
w = w - weight
# 2、背包重量小于最优商品重量,则拿走背包剩余容量的商品
else:
m[idx] = w / weight
total_value = total_value + price * m[idx]
w = 0
return total_value, m
print(fractional_backpack(goods, 50)) # 小偷背包50千克
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# 3. 贪心算法基础示例-拼接最大数字问题
有n个非负整数,将其按照字符串拼接的方式拼接为一个整数。如何拼接可以使得得到的整数最大?
贪心结论:比较字符串,通过冒泡排序相加二个字符串进行比较
- 例如:32,94,128,1286,6,71可以拼接出的最大整数位94716321286128
"""
拼接最大数字问题
有n个非负整数,将其按照字符串拼接的方式拼接为一个整数。如何拼接可以使得得到的整数最大?
- 例如:32,94,128,1286,6,71可以拼接出的最大整数位94716321286128
比较字符串的大小
'32' > '128' 比较首字母大小,如果首字母一直,则比较后一位
思路:
1、采用字符串比较的方式
2、通过冒泡排序的方式进行排序,y+x if y+x > x+y else x+y
每二个元素分别相加,然后通过冒泡排序进行排序,这里用了sort,在自定义排序规则
"""
import functools
print('32' > '128') # True
print('3266' > '328') # False
li = [32, 94, 128, 1286, 6, 71]
def custom_rules(y, x):
"""自定义排序规则,分别对元素的每一个值相加,比较字符串得到最大值排序"""
if y + x < x + y: # 31 + 32 3132 3231
return 1
elif y + x > x + y: # 32 + 31 3231 3132
return -1
else: # 两个元素相加相等的情况 11 + 11 = 1111
return 0
def number_join(li):
"""
拼接最大数字问题
:param li: 列表
:return: 最大数
"""
li = list(map(str, li)) # 将列表的每一个元素转成字符串
li.sort(key=functools.cmp_to_key(custom_rules)) # functools.cmp_to_key自定义函数,比lambda功能多(通过自定义规则排序)
return ''.join(li)
print(number_join(li))
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# 4. 贪心算法基础示例-活动选择问题
假设有n个活动,这些活动要占用同一片场地,而场地在某时刻只能供一个活动使用。每个活动都有一个开始时间Si和结束时间Fi(题目中时间以整数表示),表示活动在【Si,Fi)区间占用场地
贪心结论:最先结束的活动一定使最优解的一部分(先按照结束时间排序,只要是当前的活动的开始时间,大于等于最后一个活动的结束时间,就是不冲突)
- 证明:假设a是所有活动中最先结束的活动,b是最优解中最先结束的活动。
- 如果a=b,结论成立。
- 如果a!=b,则b的结束时间一定晚于a的结束时间,则此时用a替换掉最优解中的b,a一定不与最优解中的其他活动时间重叠,因此替换后的解也是最优解。
问:安排那些活动能够使该场地举办活动的个数最多?

"""
假设有n个活动,这些活动要占用同一片场地,而场地在某时刻只能供一个活动使用。每个活动都有一个开始时间Si和结束时间Fi(题目中时间以整数表示),表示活动在【Si,Fi)区间占用场地
**贪心结论:最先结束的活动一定使最优解的一部分(先按照结束时间排序,只要是当前的活动的开始时间,大于等于最后一个活动的结束数据就是不冲突)**
- 证明:假设a是所有活动中最先结束的活动,b是最优解中最先结束的活动。
- 如果a=b,结论成立。
- 如果a!=b,则b的结束时间一定晚于a的结束时间,则此时用a替换掉最优解中的b,a一定不与最优解中的其他活动时间重叠,因此替换后的解也是最优解。
**问:安排那些活动能够使该场地举办活动的个数最多?**
思路:
1、先以活动结束时间排序
"""
active_time_period = [(1, 4), (3, 5), (0, 6), (5, 7), (3, 9), (5, 9), (6, 10), (8, 11), (8, 12), (2, 14), (12, 16)]
active_time_period.sort(key=lambda x: x[1])
def activity_selection(active_time_period):
"""
活动选择问题
:param active_time_period: 活动列表
:return: 最优活动列表
"""
optimal = [active_time_period[0], ] # 最优活动(已经通过结束时间排序)
for i in range(1, len(active_time_period)):
if active_time_period[i][0] >= optimal[-1][1]: # 当前的活动的开始时间,大于等于optimal最后一个活动的结束数据就是不冲突
# 因为上面以及通过结束时间排好序的,只要是不冲突就是最优活动
optimal.append(active_time_period[i])
return optimal
print(activity_selection(active_time_period))
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 5.2 动态规划
https://zhuanlan.zhihu.com/p/365698607
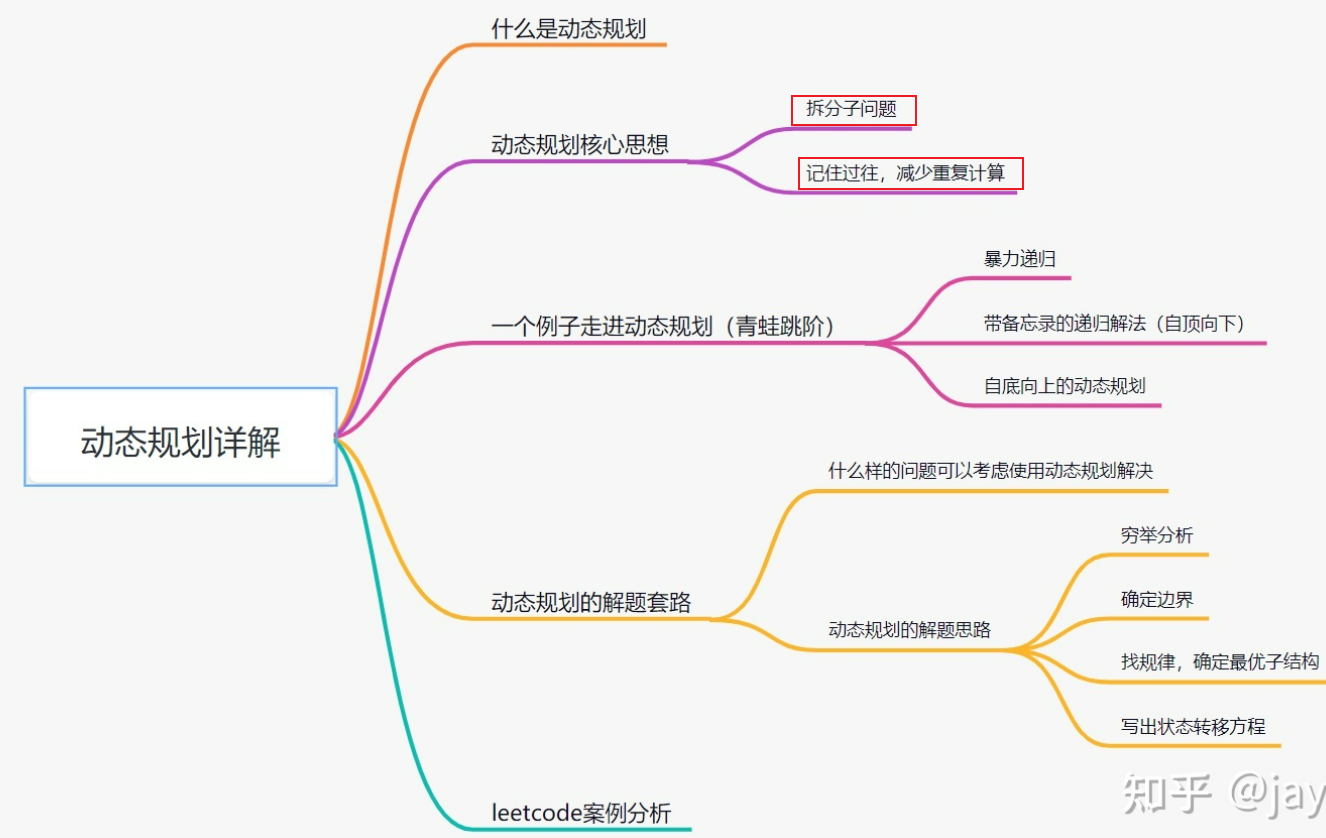
!动态规划例题(重点看这个)
https://blog.csdn.net/hollis_chuang/article/details/103045322
# 1、动态规划基础
什么是动态规划?
动态规划(英语:Dynamic programming,简称 DP)动态规划其实就是,给定一个问题,我们把它拆成一个个子问题,直到子问题可以直接解决。然后呢,把子问题答案保存起来,以减少重复计算。再根据子问题答案反推,得出原问题解的一种方法。
动态规划核心思想
动态规划最核心的思想,就在于拆分子问题,记住过往,减少重复计算。
- 拆分子问题
- 记住过往,减少重复计算
例子
我们来看下,网上比较流行的一个例子:
A : "1+1+1+1+1+1+1+1 =?"
A : "上面等式的值是多少"
B : 计算 "8"
A : 在上面等式的左边写上 "1+" 呢?
A : "此时等式的值为多少"
B : 很快得出答案 "9"
A : "你怎么这么快就知道答案了"
A : "只要在8的基础上加1就行了"
A : "所以你不用重新计算,因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"
2
3
4
5
6
7
8
9
10
11
# 2、示例
# 2.1 动态规划示例-斐波那契数列
斐波那契数列(公式):Fn = Fn-1 + Fn-2
练习:使用递归和非递归的方法来求解斐波那契数列的第n项
一般这些子问题很相似,可以通过函数关系式递推出来。然后呢,动态规划就致力于解决每个子问题一次,减少重复计算,比如斐波那契数列就可以看做入门级的经典动态规划问题。
实现动态规划二个条件:
- 1、拆分子问题: 比如斐波那契数列就有一个规律公式:Fn = Fn-1 + Fn-2
- 2、记住过往: 减少重复计算,把执行过的存放到列表中
"""
斐波那契数列(公式):Fn = Fn-1 + Fn-2
练习:使用递归和非递归的方法来求解斐波那契数列的第n项
递归的方式:就会重复执行一些步骤
比如:
f(3) = f(2) + f(1)
f(4) = f(3) + f(2) # 重复计算f(2)
f(5) = f(4) + f(3) # 重复计算f(3)
"""
def fibonacci(n):
"""递归实现斐波那契数列"""
if n == 1 or n == 2:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)
print(fibonacci(5))
def fibonacci_no_svr(n):
"""非递归实现斐波那契数列
实现动态规划二个条件:
1、拆分子问题: 比如斐波那契数列就有一个规律公式:Fn = Fn-1 + Fn-2
2、记住过往: 减少重复计算,把执行过的存放到列表中
"""
fib = [0, 1, 1] # 因为是从下标0开始,所有前面加个0补位,记录计算过后的值
if n > 2:
for i in range(n - 2): # n-2的原因是斐波那契数列的前二个都是1,从第三个开始计算相加的值
f = fib[-1] + fib[-2] # 列表的后两项相加,添加到列表,存入计算过后的值
fib.append(f)
return fib[n] # 返回第n项的值
print(fibonacci_no_svr(100))
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
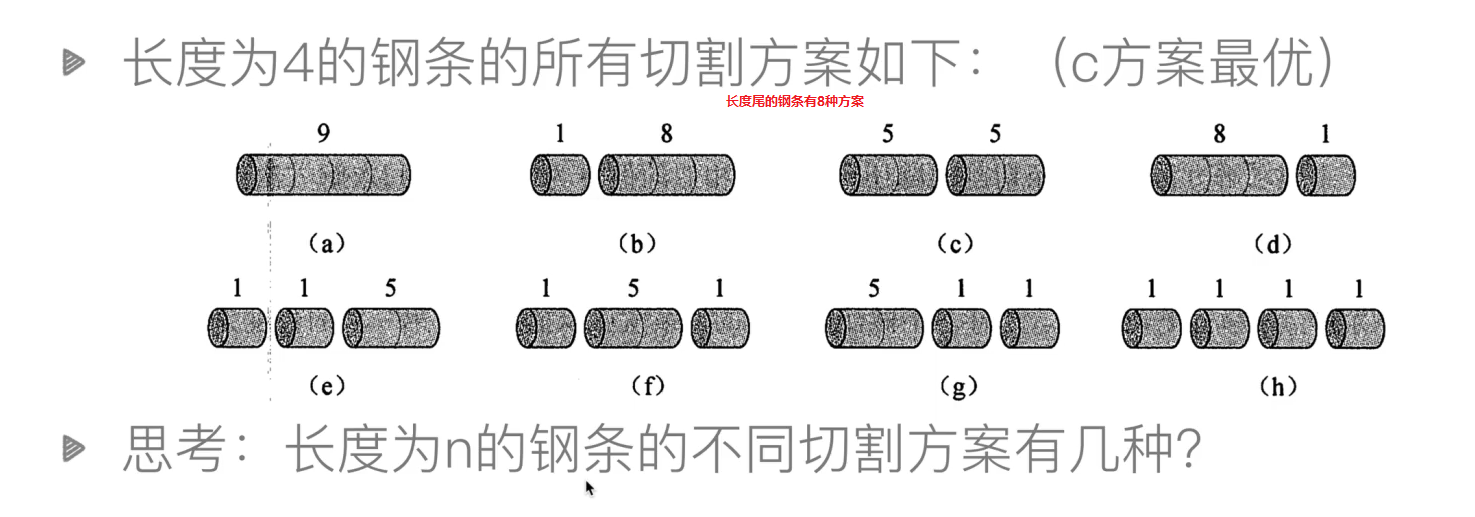
# 2.2 动态规划示例-钢条切割问题
https://blog.csdn.net/u013309870/article/details/75193592

# 5.3 最长公共子序列
# 5.4 偶几里得算法
# 1、最大公约数
- 约数:如果整数a能被整数b整除,那么a叫做b的倍数,b叫a的约数。
- 给定两个整数a,b,两个数的所有公共约数中的最大值即为最大公约数。例如:12与16的最大公约束是4
偶几里d得算法:gcd(a,b) = gcd(b,a mod b)
对两个不全为0的非负整数不断应用此式:gcd(m,n)=gcd(n,m mod n);直到m mod n为0时。m就是最大公约数
例如:
gcd(60,21) = gcd(21,18) = gcd(18,3) = gcd(3,0) = 3 # 当b等于0得时候 a就是,二个数得最大公约数
2
3
"""
偶几里d得算法:**gcd(a,b) = gcd(b,a mod b)**
例如:
gcd(60,21) = gcd(21,18) = gcd(18,3) = gcd(3,0) = 3 # 当b等于0得时候 a就是,二个数得最大公约数
"""
def mct(a, b):
"""递归实现二数最大公约数"""
if b == 0:
return a
else:
print(a, b)
return mct(b, a % b)
print(mct(60, 21))
def mct_no_svr(a, b):
"""while实现二数最大公约数"""
while b != 0:
c = a % b
a = b
b = c
return a
print(mct_no_svr(60, 21))
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 2、分数的四则运算
利用欧几里得算法实现一个分数类,支持分数的四则运算。
class Fraction:
def __init__(self, a, b):
self.a = a
self.b = b
x = self.gcd(a, b) # 最大公约数
# 得到分数的最简分式
self.a /= x
self.b /= x
# 计算最大公约数
def gcd(self, a, b):
while b > 0:
r = a % b
a = b
b = r
return a
# 计算最小公倍数
def zgs(self, a, b):
# 12 16 --> 4
# 3 * 4 * 4 = 48
x = self.gcd(a, b)
return a * b / x
# 分数相加
def __add__(self, other):
# 1/12 + 1/20
a = self.a
b = self.b
c = other.a
d = other.b
# 分母
denominator = self.zgs(b, d)
# 分子
molecule = a * (denominator / b) + c * (denominator / d)
return Fraction(molecule, denominator)
def __rdivmod__(self, other):
pass
def __str__(self):
return "%d/%d" % (self.a, self.b)
# 实现分数的加法
a = Fraction(1, 3) # 1/3
b = Fraction(1, 2) # 1/2
print(a + b) # 1/3 + 1/2
print(a-b)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
# 5.5 RSA算法介绍
# 1、密码与加密
- 传统密码:加密算法是密码的
- 现代密码系统:加密算法是公开的,密匙是秘密的
- 对称加密
- 非对称加密
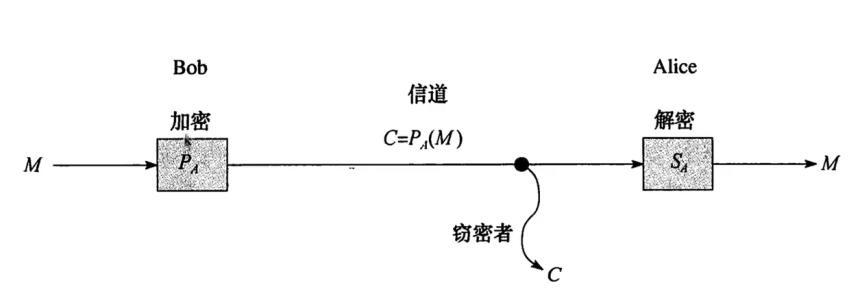
RSA非对称加密系统
- 公钥:用来加密,是公开的
- 私钥:用来解密,是私有的

